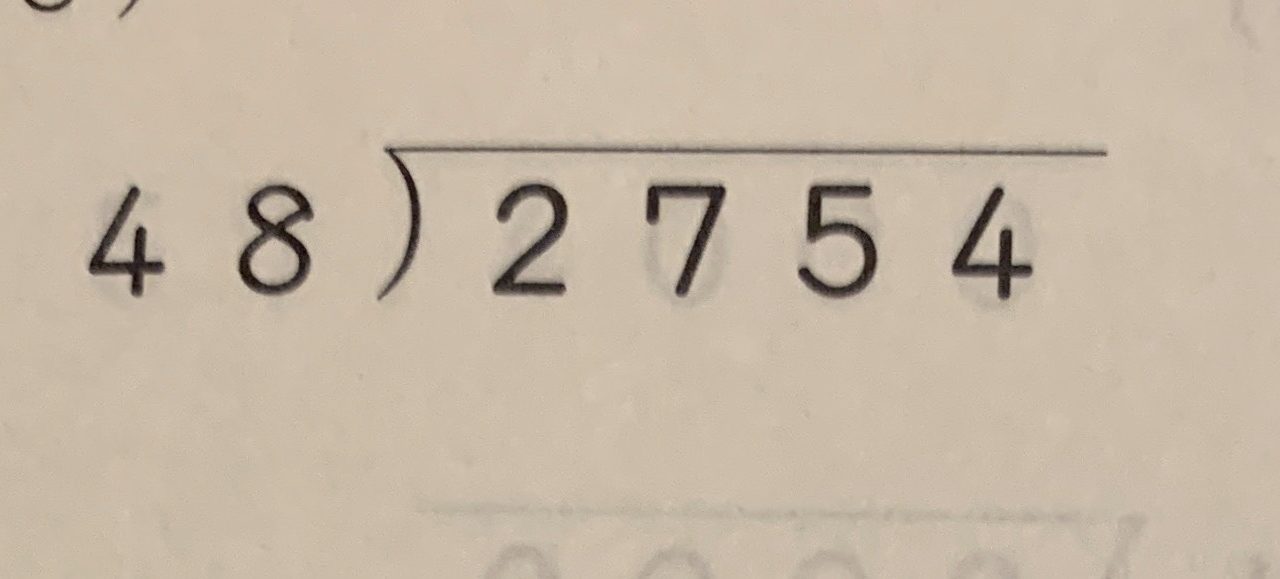今回の投稿では、前回の内容を受けて、英語教育の具体的な教材を書くつもりでしたが、長女が突然これまで順調にやってきていた公文の算数でつまづき、その理由が「え?こんなことが解決の糸口だったの!?」という意外なものだったので、もしかしたら同じようなお子さんいらっしゃるのではないかと思い、今回はこちらのことを書くことにしました。
まず、長女は国語に比べて算数は割と好きで、あー大変大変とは言いつつ、本当に大変で嫌というよりは、こんなところまで進んじゃったのよ~まったく~みたいな、どちらかというと、大変大変も好きのうち(ちょっと違うけど笑)みたいな感じで、本当にもう嫌!ということは殆どなかったと思いますが、今回は非常に嫌そうで、国語をイソイソとやって、算数はいつまでも進まない、、みたいな日が数日続きました。
ん?なんか様子がおかしいぞ、と思って、聞いてみると、本当に分からない。と言う。
そこで娘の異変に気付き、普段に勝手にやらせていて親が介入することはない公文を久しぶりに一緒に見てみると
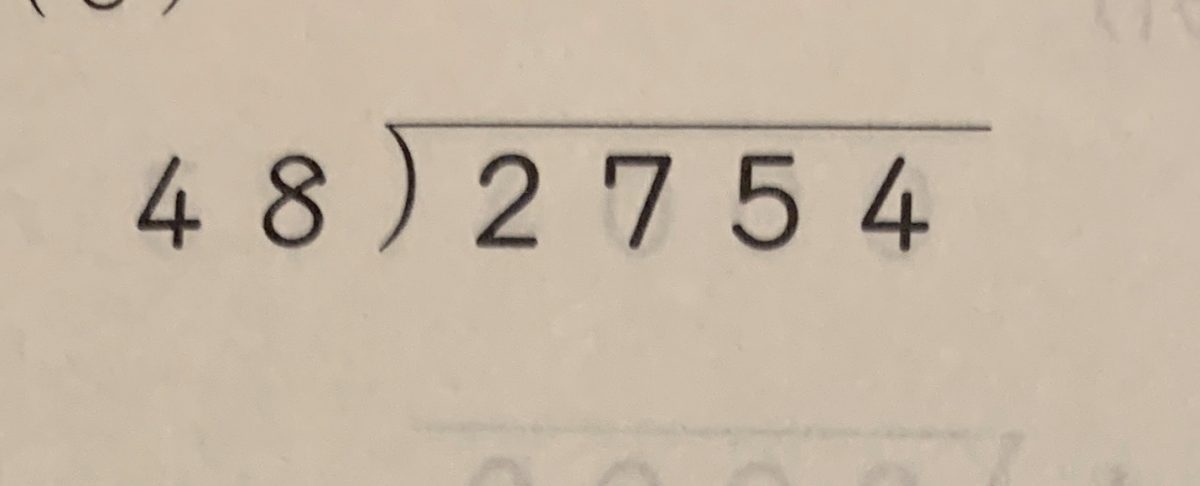
このような一見少し面倒くさそうな割り算の筆算がありました。
しかし、例えば70÷32のような一桁ずつではない割り算も問題なくしていたのに、なぜ突然難しく感じて、手につかなくなったのかを聞くと、
「えーだって〇ちゃん、2754÷48なんて分からないもん」
という、まあ、なんとも言えない漠然とした答えが返ってきました。
娘が出来なかった理由は全て、この的を得ない答えに集約されています。
「ねえ、最初から2754÷48をするんじゃないよ、まず見なくちゃいけないのは、割る方が2桁なら(この場合48)割られるほうもほうも2桁だけよ?」
というと、ほえ?という、そうなの?みたいな顔。
つまり、この場合、最初に着目するのは
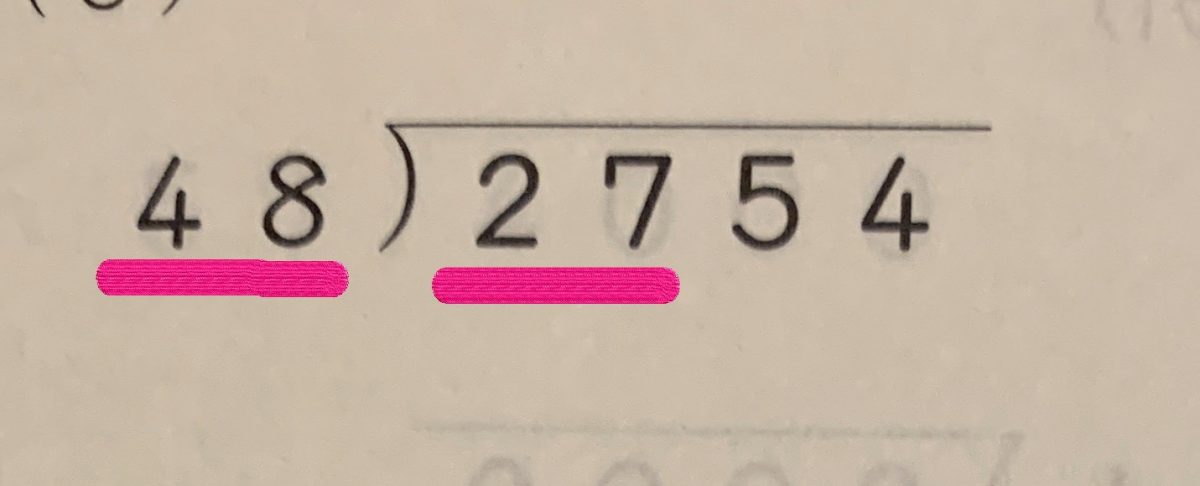
これだけ。
ただ、この場合、27より48が大きいので、もう一つ隣りまで入れて考える。
つまり、
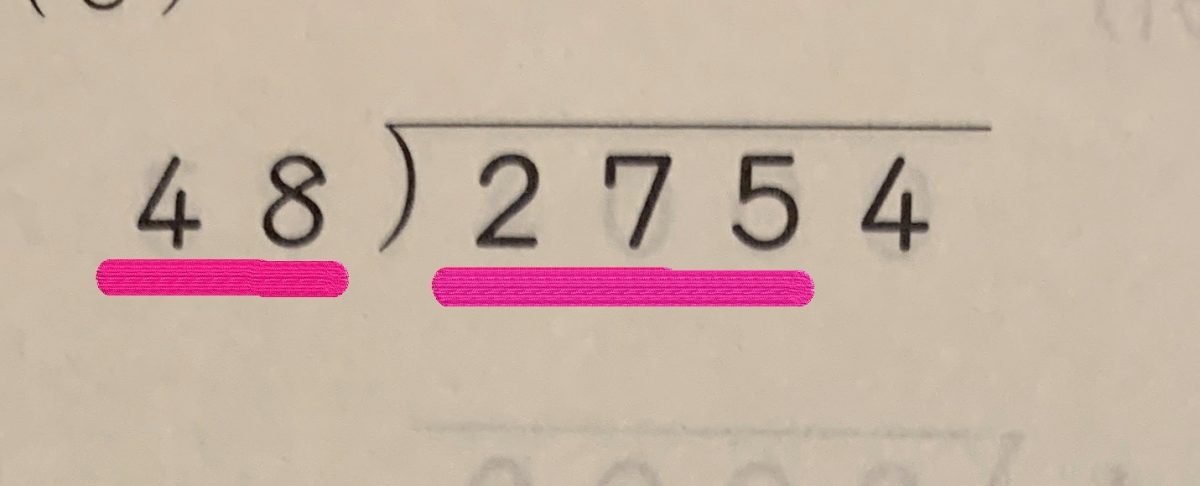
こうなると、娘の顔が曇り「ほら、やっぱり分からないじゃん」みたいな感じに。
でも、
「275と48を比べる必要ない。ここで見るのは十桁までの数字で割るなら十桁の方の数字だけ。割られる方も大きい方の桁の数字だけ!」
というと、もはや何のこっちゃ?みたいな顔に。
まず
①27と48を比べたら48の方が大きかったので27ではなく、275までで考える、この時、2754の5と4の間に頭の中で線を引く

②次に見るのは割る方の一番大きな桁の数。この場合は4。対して割られる方も大きい桁の数だけ。この場合27。
↓
つまり、27÷4をすれば良い。4×7=28でオーバーしてしまうので、
最有力候補は4×6=24の[6]
次席が4×5=20の[5]。
あとは一の桁の数次第。
③ここで48の一桁の方の数(8)を気にする。
現在の最有力候補が6だけど、8×6をしてみると48となるので、これは超えてしまいそうだ(288になってしまう)、、と予測
次席候補の5で考えると、8×5=40となり、②で出した数と合わせて240となるので、これだ!ということになる。
④次に275-240=35をして、次の段階354÷48をするけど、今回も着目するのは35と4のみ。
前述の①から③の過程を繰り返すと7あまり18という答えが出る。
このやり方を徹底して、2,3個問題を解いていくうちに、娘の頭の中で散らばっていたものが整理整頓されたらしく、また普段のように算数ができるようになりました。
つまり、娘が出来ていなかったのは、文章ーこの場合計算ですがーに句読点を打つこと。最レベについて書いた時、一番難しいのは、文章問題を解くうえで、この問題にはいくつの手順=式が存在するのか、それを読み解くことが問題を解くカギ、自分の頭の中で手順の整理が必要なのだと書きましたが、これもまさにそれでした。
桁が多い問題は、その桁の多さから、思考がストップしてしまいがちですが、桁が増えたということは複雑になったのではない、シンプルな計算の手順が増えただけなのだということを知っていなければなりません。
つまり、桁数の多い計算問題は、与えられた問題を「シンプルな計算」にすることのトレーニングなんだと知れば、あとは脳みその柔らかい子供のこと、ゲーム感覚で出来ます。
どんな風にやったら、シンプルな数字になるのか、シンプルにさえなれば、答えの候補は多くて2つしかない(先ほどの問題で候補が2つだったように)ため、慣れれば暗算でだいたいの目ぼしがつけられるようになり、書いては間違い、消しゴムで消してまた書いて、ではなく、ある程度暗算で目算をたてて、書くのは一度にできれば、スピードも、結果的に精度もぐっと上がります。
娘は今では一時期落ち込んでいた算数への士気も戻り、かかっていた時間もぐっと短縮することができています。
もし、お子様の中に同じようなところでつまづいてしまっている方がいらしたら、是非、「問題をシンプルなものにかえて考えること」そして「桁が増えたことは手順が増えただけで、複雑になったのではないこと」を話してあげてみてください!
しぇんこ
7歳と3歳の姉妹を持つアラフォー&ワーキングママです。
女の子育児をこよなく愛し、育児に仕事に家事にと奮闘中。
女の子育児ならではの悩み、4歳差ならではの悩みに向かい合い、研究の日々。
長女誕生以来、自分なりにこだわって調べてきたことを、育児に奮闘中のママへお届けしたいと思っています。
詳しい自己紹介、ブログを始めるきっかけは最初の投稿に書きました。
よろしければ、お読みくださいませ!
しぇんこ